Stack - Online Stock Span

Design an algorithm that collects daily price quotes for some stock and returns the span of that stock's price for the current day.

The span of the stock's price in one day is the maximum number of consecutive days (starting from that day and going backward) for which the stock price was less than or equal to the price of that day.

For example, if the prices of the stock in the last four days is [7,2,1,2] and the price of the stock today is 2, then the span of today is 4 because starting from today, the price of the stock was less than or equal 2 for 4 consecutive days.
Also, if the prices of the stock in the last four days is [7,34,1,2] and the price of the stock today is 8, then the span of today is 3 because starting from today, the price of the stock was less than or equal 8 for 3 consecutive days.

Implement the StockSpanner class:

StockSpanner() Initializes the object of the class.
int next(int price) Returns the span of the stock's price given that today's price is price.

Input: ["StockSpanner", "next", "next", "next", "next", "next", "next", "next"]
[[], [100], [80], [60], [70], [60], [75], [85]]
Output: [null, 1, 1, 1, 2, 1, 4, 6]
Explanation:
StockSpanner stockSpanner = new StockSpanner();
stockSpanner.next(100); // return 1
stockSpanner.next(80); // return 1
stockSpanner.next(60); // return 1
stockSpanner.next(70); // return 2
stockSpanner.next(60); // return 1
stockSpanner.next(75); // return 4, because the last 4 prices (including today's price of 75) were less than or equal to today's price.
stockSpanner.next(85); // return 6

Constraints:

1 <= price <= 10⁵
At most 10⁴ calls will be made to next.

Solution 1 - Using stack, construct a monotonically decreasing stack

In this approach, we are going to build a monotonically decreasing stack, meaning that elements in the stack should be in a decreasing order, when we see a number higher than the top of the stack, then we delete elements from stack to ensure that the stack is still monotonically decreasing order.

Let's understand this with an example prices = [100, 80, 60, 70, 60, 75, 85]

To start with, lets declare a stack that we will be using to store price and its span as pair of numbers.
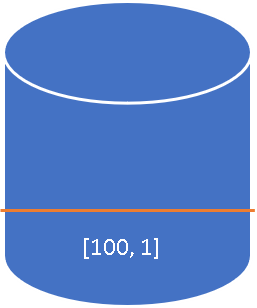
First element price is 100 and the stack is empty, so the span for this price is 1. So, we will add [100,1] as a pair into the stack (price , its span).

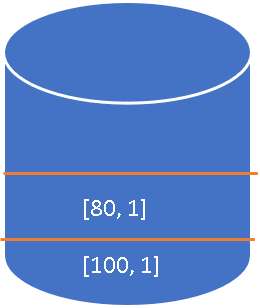
Second element price is 80, and the stack's top element is greater than this, so the span for this is going to be 1. So, we will add [80,1] into the stack.

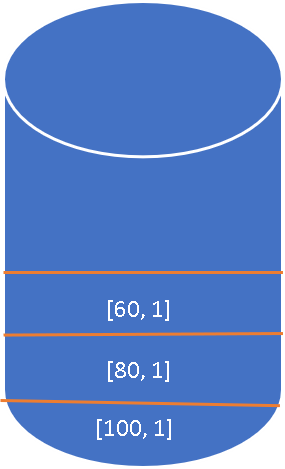
Third element price is 60, and the stack's top element is greater than this, so the span for this is going to be 1. So, we will add [60,1] into the stack.

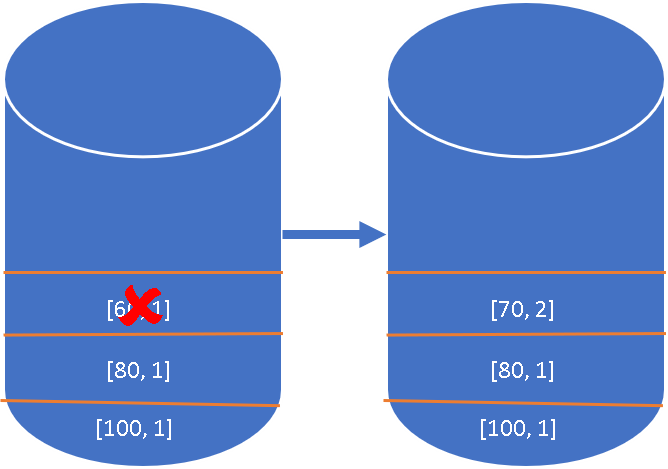
Fourth element price is 70, and the stack's top element 60 is less than this, so take the span of previous smaller element, and add it to current elements span, so the span becomes 2, we will check next element from the stack, it is 80, since this is greater than 70, we don't do anything. We will just remove the smaller element that we found, i.e. 60 and add [70,2] into the stack.

Fifth element price is 60, and the stack's top element is greater than this, so the span for this is going to be 1. So, we will add [60,1] into the stack.

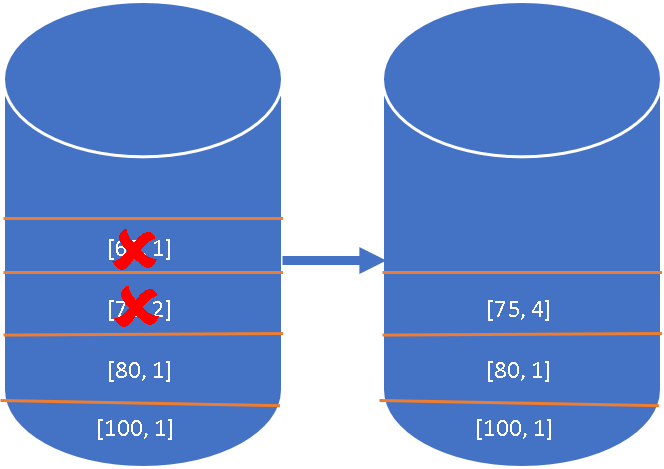
Sixth element price is 75, and the stack's top element 60 is less than this, so take the span of previous smaller element, and add it to current elements span, so the span becomes 1 (current element) + 1 (previous smaller) = 2, we will check next element from the stack, it is 70, this is also smaller, so take the span of previous smaller element, and add it to current elements span, so the span becomes 2 (current) + 2 (previous) = 4, next element from the stack is 80, since this is greater than 75, we don't do anything. We will just remove the smaller elements that we found, i.e. 60 and 70, and add [75,4] into the stack.

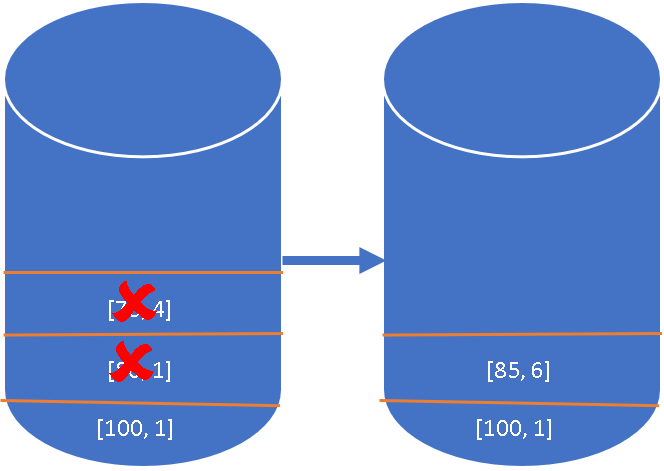
Sixth element price is 85, and the stack's top element 75 is less than this, so take the span of previous smaller element, and add it to current elements span, so the span becomes 1 (current element) + 4 (previous smaller) = 5, we will check next element from the stack, it is 80, this is also smaller, so take the span of previous smaller element, and add it to current elements span, so the span becomes 5 (current) + 1 (previous) = 6, next element from the stack is 100, since this is greater than 85, we don't do anything. We will just remove the smaller elements that we found, i.e. 75 and 80, and add [85,6] into the stack.

Since we are constructing a monotonically decreasing stack, each time a larger element found, we are going back into the stack until the elements that are smaller or equal to this, then replacing all smaller elements prior with current one, so for the next element which larger than current, we are not going back again to all the way to all prior smaller elements, so the time complexity is going to be O(n).

Implementation steps:

First, we will create a variable priceSpanPair a Stack which will store stock price and the span as a pair of numbers.
Next, each time a next(int stock) method is called, calculate the span using the below logic:

Initalize a variable span = 1, then look at spans from priceSpanPair stack and if the stock price is less than current one, then add that span to current span. For example if previous stock is 10 and the current stock is 11, we can add previous span count as well.
If the previous price's span is added, i.e. if the previous price is less than or equal to current price, we can remove that element from priceSpanPair and add current element along with its span as a pair. This is an important step, because if the current price is less than previous price, there is no need to remove previous element and the span for current pday price is going to be 1, but whenever the next bigger price is seen, we can add span from previous prices in a cumulative fashion, and remove previus elements, so that the loopup range for next element is already pre-computed.

Return span as the answer.

import java.util.Stack; public class StockSpanner { final Stack<int[]> priceSpanPair; // each array will have two values -> price, span public StockSpanner() { priceSpanPair = new Stack<>(); } public int next(int price) { int span = 1; while(!priceSpanPair.isEmpty() && priceSpanPair.peek()[0] <= price) { span += priceSpanPair.peek()[1]; priceSpanPair.pop(); } priceSpanPair.push(new int[]{price, span}); return span; } public static void main(String[] args) { StockSpanner stockSpanner = new StockSpanner(); System.out.println(stockSpanner.next(100)); System.out.println(stockSpanner.next(80)); System.out.println(stockSpanner.next(60)); System.out.println(stockSpanner.next(70)); System.out.println(stockSpanner.next(60)); System.out.println(stockSpanner.next(75)); System.out.println(stockSpanner.next(85)); } }

Complexity Analysis:

Time complexity: Above code runs in O(n) time where n is the number of times next method is called.
Space complexity: O(n) for the stack.

Above implementations source code can be found at GitHub link for Java code

Constraints:

Contents

Implementation steps:

Complexity Analysis: