Dynamic Programming - Traingle Minimum Path Sum

Given a 2D array triangle, which represents a triangle shaped array, return minimum path sum from top to bottom.

For each step, you may move to an adjacent index number of the row below. More formally, if you are on index i on the current row, you may move to either index i or index i + 1 on the next row.

Note that this is not addition of minimum value from each sub array, we have to look only at i and i + 1 indexes from row below.

Input: triangle = [[2],[3,4],[6,5,7],[4,1,8,3]]
Output: 11
Explanation: The triangle looks like this
[2]
[3, 4]
[6, 5, 7]
[4, 1, 8, 3]
So, minimum path sum will be 2 + 3 + 5 + 1 = 11

Input: triangle = [[2],[6,4],[5,2,9],[2, 3, 6, 10]]
Output: 11
Explanation: The triangle looks like this
[2]
[6, 4]
[5, 2, 9]
[2, 3, 6, 10]
So, minimum path sum will be 2 + 4 + 2 + 3 = 11

Input: nums = [[-10]]
Output: -10

Solution using depth first search recursively
Solution using dynamic programming memoization

In this approach, we will compute the mininum value from adding bottom row i^th index number or (i+1)^th indexed number. Recusrively repeat the same process in bottom - up approach.

When we are at the last row, Min number will be itself as there is no row aftre that or you can assume that there is row with all 0's.
Calculate Min possible value using Min(triangle[row][column] + minimumTotal(triangle[row+1][column]), triangle[row][column] + minimumTotal(triangle[row+1][column+1]))
For example, if we visualize the recursive solution for input [[2], [3, 4], [6, 5, 7], [4, 1, 8, 3]], it looks like below diagram.

import java.util.List; public class TriangleMinPathSum { static int minimumTotal(List<List<Integer>> triangle) { return minimumTotalBruteforce(triangle, 0, 0); } static int minimumTotalBruteforce(List<List<Integer>> triangle, int row, int column) { if(row == triangle.size()) {// when we reach end row return 0; } int currentNumber = triangle.get(row).get(column); return Math.min(currentNumber + minimumTotalBruteforce(triangle, row +1, column), currentNumber + minimumTotalBruteforce(triangle, row +1, column+1)); } }

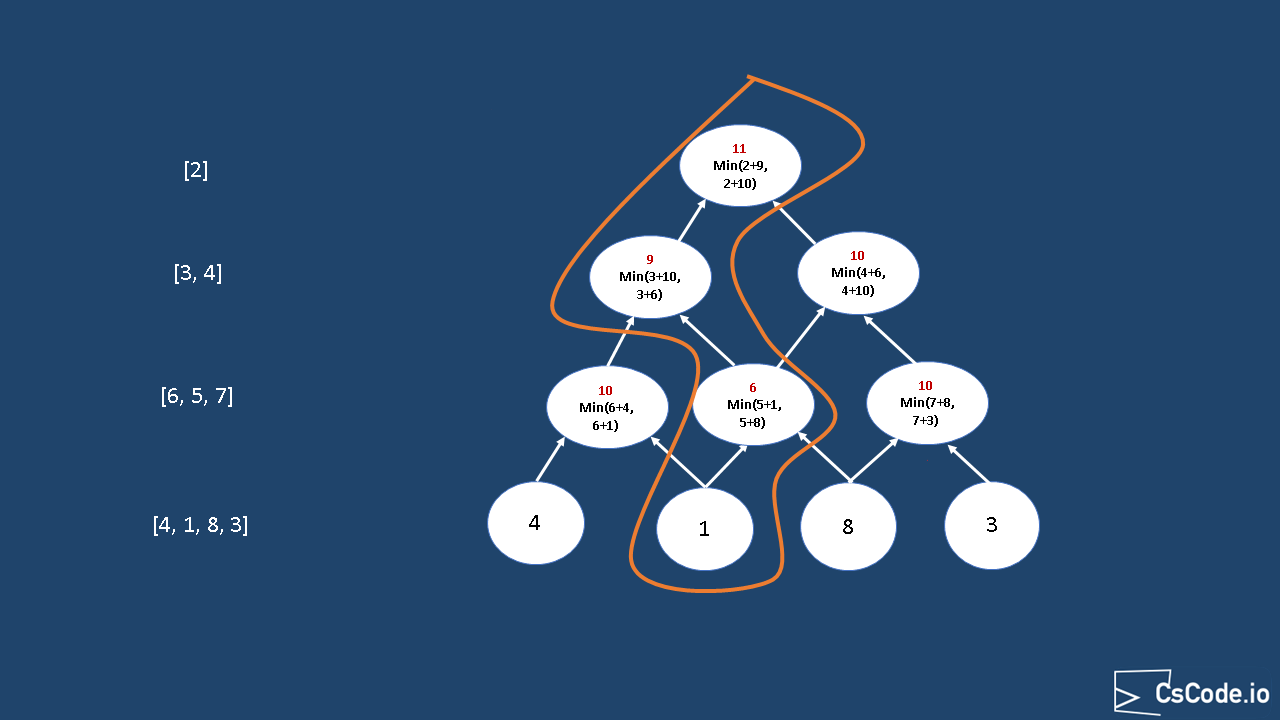
Complexity Analysis:

Time complexity: Above code runs in O(2ⁿ) time where n is the size of the array, as we are creating a decision tree with two possibilities at each step.
Space complexity: O(n) where n is the size of input array.

In this approach, we are going to solve the problem using below steps.

Create a temporary array with size as last row size +1. int[] temp = new int[triangle.get(triangle.size-1).size() + 1]
We are going to store the mininum path sum computed into this temporary array, by looking at Min(currentElement + i^th indexed number from temporary array, currentElement + i + 1^th indexed number from temporary array)
When we are done with all rows from triangle, first element in the temporary array is our answer. Calculating minimum path sum in bottom - up approach looks like below diagram.
If you notice we are only maintaining temporary array with size as last sub array size of triangle array in each iteration.

dynamic programming solution illustration

import java.util.List; public class TriangleMinPathSum { static int minimumTotalDp(List<List<Integer>> triangle) { int[] temp = new int[triangle.get(triangle.size()-1).size()+1]; for(int i= triangle.size() -1; i>=0; i--) { // start from last row bottom-up List<Integer> row = triangle.get(i); for(int j=0; j<row.size(); j++){ temp[j] = Math.min(row.get(j)+temp[j], row.get(j)+temp[j+1]); } } return temp[0]; } }

Complexity Analysis:

Time complexity: Above code runs in O(n * m) time where n is the size of the array and m is the bottom sub array size.
Space complexity: O(n) where n is the bottom sub array size.

Above implementations source code can be found at GitHub link for Java code

Contents

Complexity Analysis:

Complexity Analysis: