Dynamic Programming - Partition Equal Subset Sum

Given an integer array nums, return true if you can partition the array into two subsets such that the sum of the elements in both subsets is equal or false otherwise.

Input: nums = [1,5,11,5]
Output: true
Explanation: Input array can be partitioned with two subsets [1, 5, 5] and [11].

Input: nums = [1,2,3,5]
Output: false
Explanation: Input array cannot be partitioned into two subsets.

Solution intution
Solution using recursion
Solution using recursion and memoization
Solution using DP memoization and memory optimized

Below are two important decisions to make in the solution intution.

Compute the sum of elements from input array and if the value is an odd number, then you can simply return false, because it is not possible divide the input array into two subsets with equal sum. For example, consider the input array [1,2,3,5] and if you sum the elements it will come as 11, and it is not possible to split input array into two subsets with each sum as 5.5, so you can simply return false.
If the sum of elements from input array is an even number, then calculate sum/2 and check whether there is any subset array whose sum is equal to that.
For example [1, 5, 11, 5] will give sum as 22, and sum/2 is 11, and we can have subsets [1, 5, 5] and [11]. Another example [2,10] will give sum as 12, and sum/2 is 6, but there is no way we can have two subsets with sum as 6.

In this approach, we will compute the sum of elements from input array and check if if it even or odd, if it is odd then return false, otherwise check if there is any subset possible with sum as sum/2.

In the recursion approach, we are going to check if there is any sub set sum available with following sub problems.
- n-1 elements and sum.
- n-1 elements and sum - nums[n-1].
While solving the problem recursively, we can draw two base cases.
- If the sum is reduced to 0, then a partition is possible, so return true.
- If the number of eleemnts in array becomes empty, and the sum is stil greater than 0 or if the sum becomes less than 0, then return false.
Below is an illustration how we are going to solve this recursively.

public class PartitionEqualSubsetSum { static boolean canPartition(int[] nums) { int sum =0; for(int num: nums) { sum += num; } if(sum % 2 ==0) { return canPartitionRecursive(nums, sum/2); } return false; } static boolean canPartitionRecursive(int[] nums, int sum) { if(sum == 0) { // we have reached to a point where subset with give sum is possible return true; } if((nums.length == 0 && sum > 0) || sum <0){ // we have reached to a point where subset with give sum is not possible return false; } int[] remainder = new int[nums.length-1]; System.arraycopy(nums, 0, remainder,0,remainder.length); return canPartitionRecursive(remainder, sum) || canPartitionRecursive(remainder, sum - nums[nums.length-1]); } }

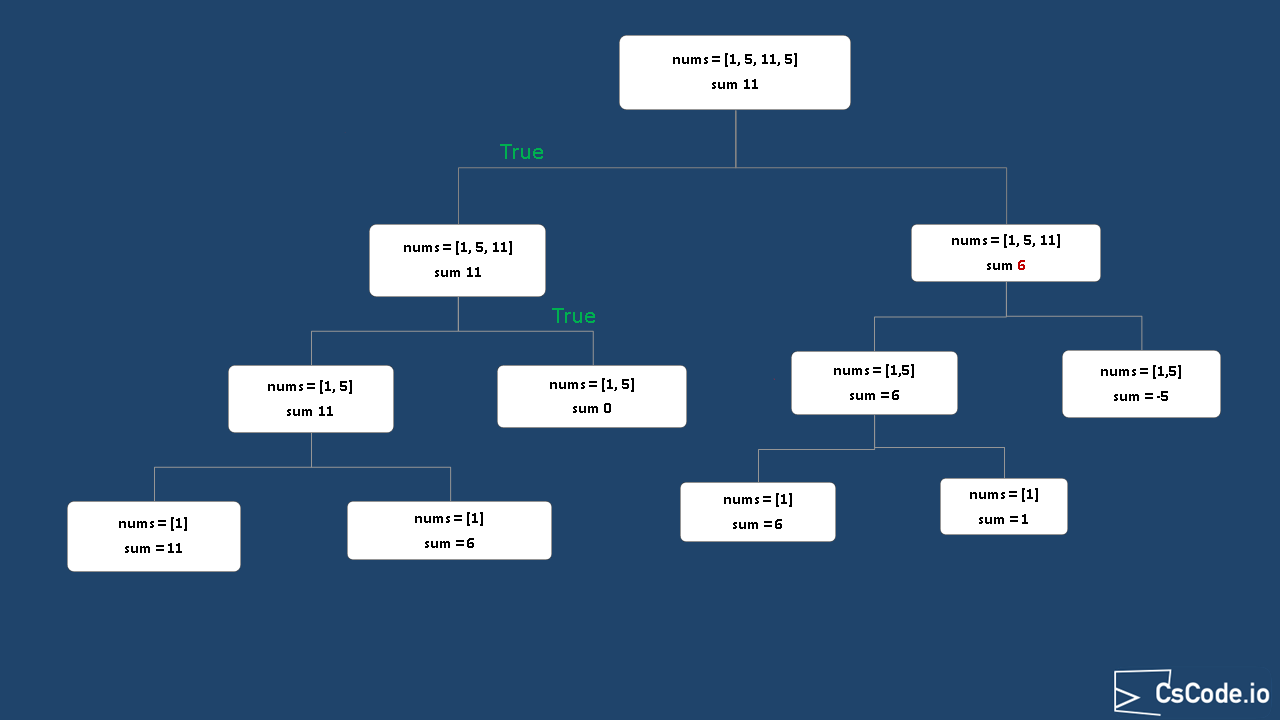
Complexity Analysis:

Time complexity: Above code runs in O(2ⁿ) time where n is the size of the array, as we are creating a decision tree with two possibilities at each step.
Space complexity: O(n²) as we are making recursive loops n times and each time we are creating a new array and copying elements. We can avoid this by supplying just the array index to the recursive function and reduce the space complexity to O(n).

As you can see in above solution, sub problems will be repeated (for example, circled sub problems in the below diagram), so we can cahe the sub problem answer and use it.

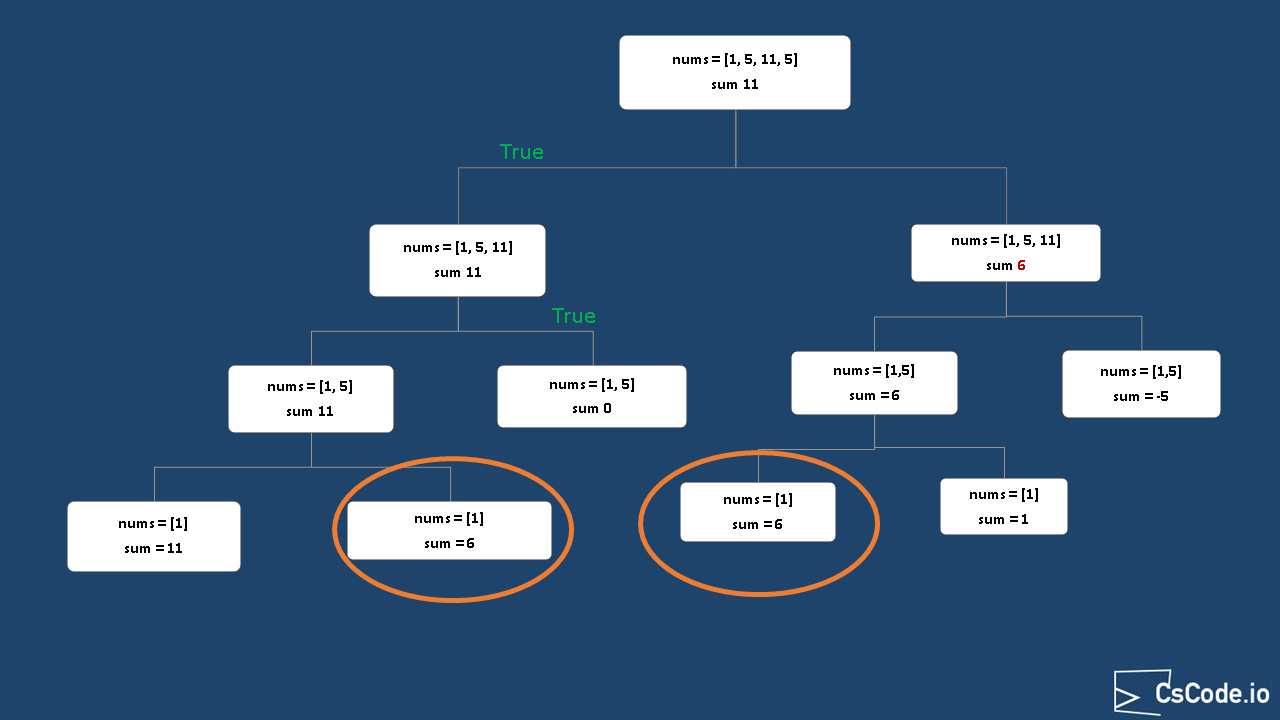
recursive solution with memoization illustration

In this approach of memoization, we are going to cache the sub problem results with key as current length of input array, sum and its result into a HashMap.
When the sub problem answer is found in the cache, we simply return that, if not then we call the function recursively and cache it.

import java.util.HashMap; public class PartitionEqualSubsetSum { /* optimized logic using memoization */ static boolean canPartitionUsingMemoization(int[] nums) { int sum = 0; for (int num : nums) { sum += num; } if (sum % 2 == 0) { HashMap memoize = new HashMap<>(); return canPartitionRecursive(nums, sum / 2); } return false; } static boolean canPartitionUsingMemoizationRec(int[] nums, int reminderArrayLength, int sum, HashMap cache) { if (sum == 0) { return true; } if ((reminderArrayLength == 0 && sum > 0) || sum < 0) { return false; } String key = reminderArrayLength + "-" + sum; if (cache.containsKey(key)) { return cache.get(key); } int reducedArrayLength = reminderArrayLength - 1; boolean ans = canPartitionUsingMemoizationRec(nums, reducedArrayLength, sum, cache) || canPartitionUsingMemoizationRec(nums, reducedArrayLength, sum - nums[reducedArrayLength], cache); cache.put(key, ans); return ans; } }

Complexity Analysis:

Time complexity: Above code runs in O(sum * n) time where n is the size of the array.
Space complexity: O(sum * n) as there may be need for cache every answer.

In this approach, we are going to compute all possible sums for each number in the array and store them in a Set. At the end return true if the set contains sum/2, false otherwise.

import java.util.HashMap; import java.util.HashSet; public class PartitionEqualSubsetSum { /* similar to above, but optimized */ static boolean canPartitionOptimizedUsingDP(int[] nums) { int sum = 0; for(int num: nums) { sum += num; } if(sum % 2 == 0) { return canPartitionMemoryOptimizedUsingDP(nums, sum/2); } return false; } static boolean canPartitionMemoryOptimizedUsingDP(int[] nums, int sum) { HashSet<Integer> memoized = new HashSet<>(); memoized.add(0); for(int i=0; i<nums.length; i++) { HashSet<Integer> nextSet = new HashSet<>(); for(Integer val : memoized) { nextSet.add(val+nums[i]); nextSet.add(val); } memoized = nextSet; } return memoized.contains(sum); } }

Complexity Analysis:

Time complexity: Above code runs in O(sum * n) time where n is the size of the array.
Space complexity: O(sum) as the max size of the set can be the sum.

Above implementations source code can be found at GitHub link for Java code

Contents

Complexity Analysis:

Complexity Analysis:

Complexity Analysis: