DP - Longest Palindrome Substring

Given a string s, return the longest palindromic substring in s.

A string is palindromic if it reads the same forward and backward. For example abcba is a palindromic string that expands from center letter c and abba is also a palindromic string that expands with no center letter.

Input: s = "babad"
Output: "bab" or "aba"
Explanation: there are two longest palindromic substring in the input "bab" and "aba" and both are of length 3, so you return any one of them.

Input: s = "cbbd"
Output: "bb"
Explanation: longest palindromic substring is "bb".

Solution 1 - using brute force approach
Solution 2 - expand around center

In this approach, we will generate all possible substrings, then for each substring check if that is a valid palindrome.

We will create a function bruteForceApproach that takes s as input string.
Then, we will create all possible substrings using two for loops. for(int i=0; i<s.length(); i++) { for(int j=i; j<=s.length(); j++) { String sub = s.substring(i,j); } }
Create another helper function isPalindrome that takes a String str as argument and it checks whether the given string is a palindrome or not.
- When checking whether input string is palindrome or not, there are two possibilities, when the string is an odd length string and when the string is even length string.
- Create two variables i and j to check characters on left and right side from the index where palindrome is explanding.
- When input string is odd length string, we take the mid index mid = str.length() /2, and set i=mid-1 and j=mid+1, this is because when the string length is odd, then the mid index will be the center indexed element and we will checking whether it is palindromic string from the center.
  For example, consider string "abcba", in this case mid = 5/2 which is 2, that is nothing but the center indexed character c. We wil be expanding around that center index, so we can set i=1 and j=3.
- When input string is even length string, we take the mid index mid = str.length() /2, and set i=mid-1 and j=mid, this is because when the string length is even, there is no center indexed element for the palindrome. So, we have the check middle two characters and check whether they are same, and then expand around those two characters.
  For example, consider string "abba", in this case mid = 4/2 which is 2, that is nothing but the right indexed element from the middle two elements. We wil be expanding around middle two elements, so we can set i=1 and j=2.
- Once we have set i and j variables, then check whether character at i^th index and j^th index are same or not, if they are same then decrement i and increment j to continue checking other characters in the string.
  If any of the characters on left and right are not same return false otherwise return true at the end.
We will call this isPalindrome for all substrings, and keep track of longest palindrome.
Finally return the longest palindrome substring found.

public class LongestPalindrome { /* brute force approach*/ static String bruteForceApproach(String s) { String longestPalindrome =""; for(int i=0; i< s.length(); i++) { for(int j=i; j<=s.length(); j++) { // we are doing j<=str.length() because substring method we are using below endIndex is exclusive String sub = s.substring(i,j); if(isPalindrome(sub) && sub.length()>longestPalindrome.length()) { longestPalindrome = sub; } } } return longestPalindrome; } static boolean isPalindrome(String str) { if(str == null || str.length() ==0) { return false; } if(str.length() ==1) { // if the string length is 1, it is a palindrome return true; } int i=0; int j=0; int length = str.length(); if(length % 2 == 0){ // when string length is even, for example "abba" it's a palindrome with no center int mid = length /2; // for "abba" mid will become 2, so we should set i=1 and j=2 (i.e. b b) // then, we can check remaining characters by moving i and j to left side and right side // of the string respectively j=mid; i=mid-1; } else { // when string length is odd, for example "abcba" it's a palindrome with c as center int mid = length /2; // for "abcba" mid will become 2, that is already center letter c // so we should set i=1 and j=3 (i.e. b b) // then, we can check remaining characters by moving i and j to left side and right side // of the string respectively j= mid+1; i = mid-1; } while (i>=0 && j<str.length()){ if(str.charAt(i) == str.charAt(j)) { i--; j++; } else { return false; } } return true; } }

Complexity Analysis:

Time complexity: Above code runs in O(n³) time where n is the length of input string, this is because we are generating all possible substrings using two for loops, that takes O(n²) and for each substring, we are checking whether it is palindrome or not and that takes O(n).
Space complexity: O(n) as we are creating substrings, and at given point of time we only have one substring.

In this approach, what we are going to do is, from every index in the string, we try to expand to the left and to the right and check whether the characters on both sides are same or not.

Create a helper method expandAroundCenterHelper that takes parameters input string s, int l and int r left and right indexes to expand around.
- In the implementation of this method, create a variable maxPalindrome to keep track maximum length palindrome found so far.
- We will then try to expand the palindromic substring using left and right indexes l and r.
- While l and r within the boundararies of input string's length, check character at l^th index and r^th indexes are same, that means we have found a palindrome, check the current length of palindrome using r-l+1 (+1 is because the indexes starts with 0) and keep updating the variable maxPalindrome if a maximum length palindrome found.
- If a palindrome substring is found, then decrement l and increment r and keep continuing as long as left and right indexes characters are same.
Now, call the helper method created above for both odd length palindromes and even length palindromes, by supplying left and right indexes as i, i for odd length palindromes, then i, i+1 for even length palindromes. Then, keep track of which palindrome is the largest one out of even / odd length palindromes returned.

l= i; r= i;

l= i; r= i+1;

For example, when you expand around center for input string "babad", it will produce below output. Below diagram only shows odd length palindromes, but the logic for even length palindromes is same, expect you start with two characters from indexes i and i+1.

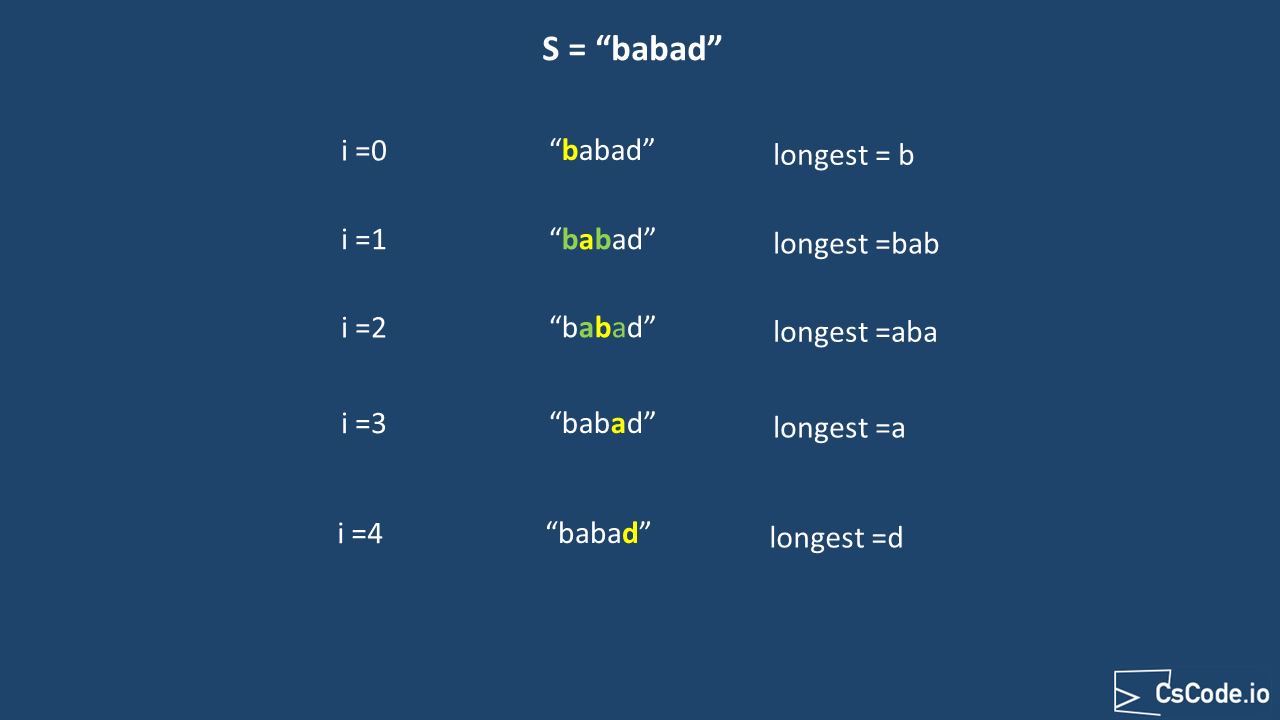
public class LongestPalindrome { /* expand around center*/ static String expandAroundCenter(String s) { String maxPalindrome = ""; for (int i = 0; i < s.length(); i++) { // this will check only odd length palindromes, because l and r pointing to same index i String maxPalindromeOdd = expandAroundCenterHelper(s, i, i); // since we have checked odd length palindromes above, we will repeat the same process for even length palindromes String maxPalindromeEven = expandAroundCenterHelper(s, i, i + 1); if (maxPalindromeOdd.length() > maxPalindrome.length()) { maxPalindrome = maxPalindromeOdd; } if (maxPalindromeEven.length() > maxPalindrome.length()) { maxPalindrome = maxPalindromeEven; } } return maxPalindrome; } static String expandAroundCenterHelper(String s, int l, int r) { String maxPalindrome = ""; while (l >= 0 && r < s.length() && s.charAt(l) == s.charAt(r)) { if (r - l + 1 > maxPalindrome.length()) { maxPalindrome = s.substring(l, r + 1); } l--; r++; } return maxPalindrome; } }

Complexity Analysis:

Time complexity: Above code runs in O(n²) time where n is the length of the input string. For every index in the string, we are expanding to the left and right side.
Space complexity: O(n), since we have to keep track of maximum length palindrome substring.

Above implementations source code can be found at GitHub link for Java code

Contents

Complexity Analysis:

Complexity Analysis: