You have n coins and you want to build a staircase with these coins.
The staircase consists of k rows where the ith row has exactly i coins.
The last row of the staircase may be incomplete.
Given the integer n, return the number of complete rows of the staircase you will build.
Input: n = 5
Output: 2
Explanation: After arranging 5 coins, 1st row will have 1 coin, 2nd row will 2 coins, and 3rd row will have 2 coins.
Since the 3rd row is incomplete, we return 2.
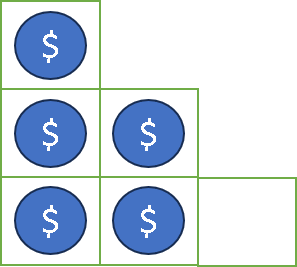 Input: n = 8
Input: n = 8
Output: 3
Explanation: Because the 4th row is incomplete, we return 3.

Constraints:
Contents
- Solution 1 - Using binary search
As per the problem statement, we have n coins and we have to arrange them in rows, like 1 coin in 1st row and 2 coins
in 2nd row and so on. So, one possible solution we can apply is, we start by subtracting number of coins needed for that row from
total number of coins n and count how many rows we can built, for example say n=10.
- 1st row requires 1 coin, so the remaining coings are 10- 1 = 9.
- 2nd row requires 2 coins, so the remaining coings are 9- 2 = 7.
- 3rd row requires 3 coins, so the remaining coings are 7- 3 = 4.
- 4th row requires 4 coins, so the remaining coings are 4- 4 = 0.
- Now there are no more coins left, so the number of rows that be built are 4.
In this solution, we have to go row by row and the time complexity is going to be ~O(n), but there is a O(log n) sulution using
Binary Search algorithm.
In this approach, we will math formula that the sum of elements from 1....n,
sum of integers formula 1+2+3+4...
sum =
Then, we apply binary search with the range of numbers 1....n. First we will initialize two pointers left =1 and right =n
and then using a while loop, compute the middle index
and compute the sum using above formula, that gives sum between 1...mid
, based on the value of sum, we can draw three conclusions.
-
If the sum at mid index is equal to n, then return the mid index, since we can built exactly mid number of rows using n coins.
-
If the sum at mid index is greater than n,
this means that we need more coins to build mid number of rows,
so we will update right index to mid-1.
-
If the sum at mid index is less than n, this means that we have more coins left after building mid number of rows,
so we will update left index to mid+1.
Finally, we will return right index as answer, since right index will be placed at the upper boundary where we have utilized all coins and
built upto right number of rows.
public class ArrangeCoins {
static int arrangeCoins(int n) {
// 1, 2, 3, 4, --- sum formula sum = n(n+1) /2
int left = 1;
int right= n;
while(left<=right) {
int mid = left + (right - left) /2;
long sum = (long)mid * (mid+1) /2;
if(sum==n) {
return mid;
} else if (sum>n) {
right = mid-1;
} else {
left = mid+1;
}
}
return right;
}
public static void main(String[] args) {
System.out.println(arrangeCoins(5));
System.out.println(arrangeCoins(8));
System.out.println(arrangeCoins(1804289383));
}
}
Complexity Analysis:
Time complexity: Above code runs in O(log n) time where n is the input number.
Space complexity: O(1).
Above implementations source code can be found at
GitHub link for Java code

