Arrays - Range Sum Query 2D Immutable

Given a 2D matrix matrix, handle multiple queries of the following type:

Calculate the sum of the elements of matrix inside the rectangle defined by its upper left corner (row1, col1) and lower right corner (row2, col2).

Implement the NumMatrix class:

NumMatrix(int[][] matrix) Initializes the object with the integer matrix matrix.
int sumRegion(int row1, int col1, int row2, int col2) Returns the sum of the elements of matrix inside the rectangle defined by its upper left corner (row1, col1) and lower right corner (row2, col2).

You must design an algorithm where sumRegion works on O(1) time complexity.

Input: Operations in this order
"NumMatrix": [[3, 0, 1, 4, 2],
[5, 6, 3, 2, 1],
[1, 2, 0, 1, 5],
[4, 1, 0, 1, 7],
[1, 0, 3, 0, 5]]
"sumRegion" : [2, 1, 4, 3]
"sumRegion" : [1, 1, 2, 2]
"sumRegion" : [1, 2, 2, 4]
Output:
Operation 1 "sumRegion" : 8
Operation 2 "sumRegion" : 11
Operation 3 "sumRegion" : 12
Explanation: Matrix grid will look like below

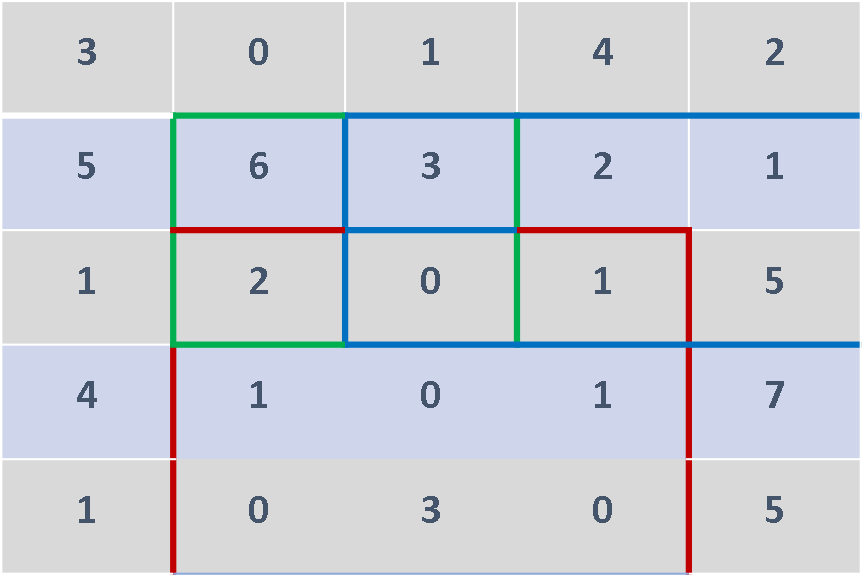Example 1

numMatrix.sumRegion(2, 1, 4, 3); // return 8 (i.e sum of the red rectangle)
numMatrix.sumRegion(1, 1, 2, 2); // return 11 (i.e sum of the green rectangle)
numMatrix.sumRegion(1, 2, 2, 4); // return 12 (i.e sum of the blue rectangle)

Constraints:

m == matrix.length
n == matrix[i].length
1 <= m, n <= 200
-10⁴ <= matrix[i][j] <= 10⁴
0 <= row1 <= row2 < m
0 <= col1 <= col2 < n
At most 10⁴ calls will be made to sumRegion.

Solution 1 - Prepare prefix-sum as part of constructor initialization

This problem is similar to Range Sum Query - Immutable, but the difference is, it takes a 2D array. So, one solution is to iterate through elements from query parameters (row1, col1) and (row2, col2).

In this approach, we are going to pre compute prefix sum inside constructor, so that we can return sumRegion in constant time.

Prefix sum implementation steps:

The way we will built prefix sum will be similar to building prefix-sum for a 1D array, but we will slightly change for 2D array, that is prefix sum at row i and column j will be computed as the sum ending at the same row plus the same column.

For example, consider the below problem, and we want to compute prefix-sum at row 1 and column 1, highlighted cell ine below diagram. Input problem - prefix sum calculation step 1 Then we would be taking the sum from the row above, plus the column before. As highlighted in below diagram. 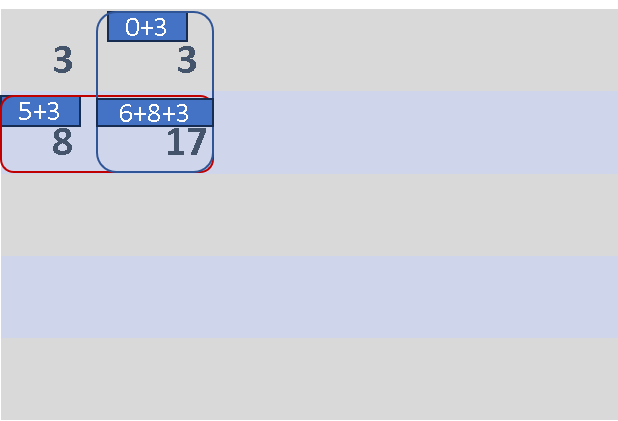When we do that,we will be double counting the element diagonally on left side, because element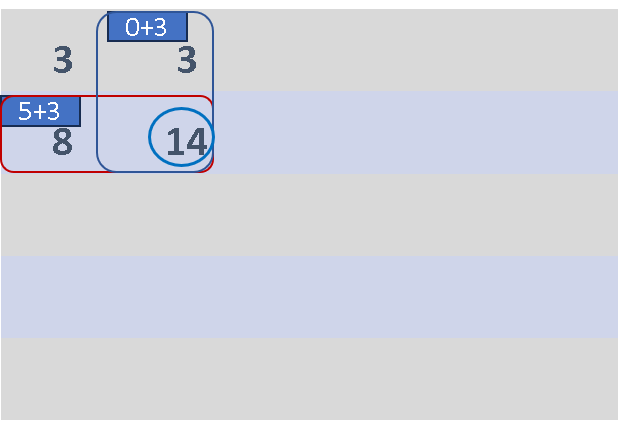 3 at (0, 0) index is counted in prefix sum calculation of (0, 1) index, as well as (1,0), so what we will do is that subtract the element at (0, 0). So, the result will become: Input problem - prefix sum calculation step 3

So, the generic formula for calculating the prefix sum at index 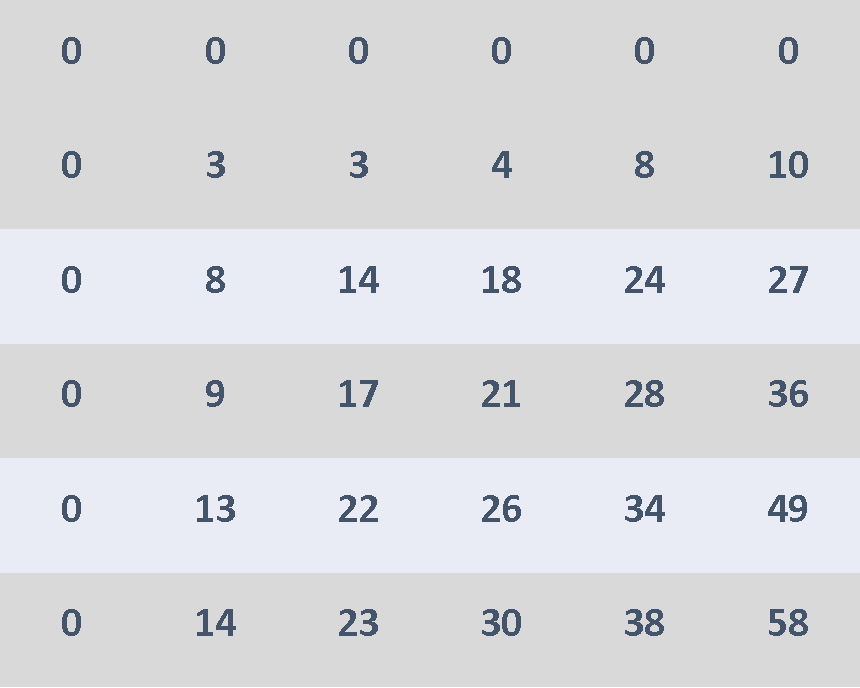(i,j) is going to be: prefixSumArray[i][j] = matrix[i-1][j-1] // current element from input array + prefixSumArray[i-1][j] // row above, same column + prefixSumArray[i][j-1] // column to left, same row - prefixSumArray[i-1][j-1]; // diagonal element in prefixSumArray, // since it was double counted in row sum and column sum We will be initializing prefixSumArray with an extra row and column, to avoid out-of-bounds when taking value from row above or column before. Prefix sum array will look like this: Input problem - prefix sum calculation step 4

sumRegion implementation steps:

Once the prefix sum array is computed, then we will get the sumRegion(row1, col1, row2, col2) as follows , we will take the value at the (row2, col2), that covers entire region starting from the index (0, 0) and until (row2, col2), then subtract the outer region that we don't want.

From the same example we computed prefix sum above, let's compute the sumRegion(1, 2, 2, 4), that is for for the highlighted region with blue color as shown in below diagram. Note that prefix sum array has additional row on top and additional column on left, so the indexes are row+1 and column+1 when referring to indexes in prefixSumArray. Input problem - prefix sum calculation step 5

So, from the cell (row2, col2), that is the cell at (2, 4) 36, we will subtract the outer regions, that is the cell at (2, 1) 17 and the cell at (0, 4) 10. so that becomes 36 - 17 - 10 = 9 . Input problem - prefix sum calculation step 6

But, notice that both cells at (2, 1) and (0, 4) have the diagonal element (0, 1), so we will add that element back into the result. Input problem - prefix sum calculation step 7 So, the result is 36 - 17 - 10 + 3 = 12 .

Generic formula calculating the sumRegion is: int row2Col2Corner = prefixSumArray[row2 + 1][col2 + 1]; // +1 is because arr has additional row and column int aboveRowCol2 = prefixSumArray[row1][col2 + 1]; int previousCol1Row2 = prefixSumArray[row2+1][col1]; int diagonalRowColumn = prefixSumArray[row1][col1]; int result = row2Col2Corner - (aboveRowCol2 + previousCol1Row2) + diagonalRowColumn ;

public class RangeSumQuery2DImmutable { private final int[][] prefixSumArray; /** * Will do the pre-computation, i.e. compute prefix array. */ public RangeSumQuery2DImmutable(int[][] matrix) { if(matrix.length == 0 || matrix[0].length == 0) { prefixSumArray = null; return; } int m = matrix.length; int n = matrix[0].length; prefixSumArray = new int[m+1][n+1]; // additional row and column with 0's for(int i=1; i<=m; i++) { for(int j=1; j<=n; j++) { prefixSumArray[i][j] = matrix[i-1][j-1] // current element from input array + prefixSumArray[i-1][j] // row above, same column + prefixSumArray[i][j-1] // column to left, same row - prefixSumArray[i-1][j-1]; // diagonal element in prefixSumArray, // since it was double counted in row sum and column sum } } /* for(int[] nums: arr) { System.out.println(Arrays.toString(nums)); }*/ } public int sumRegion(int row1, int col1, int row2, int col2) { if(prefixSumArray == null) { return 0; } int row2Col2Corner = prefixSumArray[row2 + 1][col2 + 1]; // +1 is because arr has additional row and column int aboveRowCol2 = prefixSumArray[row1][col2 + 1]; int previousCol1Row2 = prefixSumArray[row2+1][col1]; int diagonalRowColumn = prefixSumArray[row1][col1]; return row2Col2Corner - (aboveRowCol2 + previousCol1Row2) + diagonalRowColumn ; } public static void main(String[] args) { int[][] matrix = { {3, 0, 1, 4, 2}, {5, 6, 3, 2, 1}, {1, 2, 0, 1, 5}, {4, 1, 0, 1, 7}, {1, 0, 3, 0, 5} }; RangeSumQuery2DImmutable rangeSum2D = new RangeSumQuery2DImmutable(matrix); System.out.println(rangeSum2D.sumRegion(2,1, 4,3)); System.out.println(rangeSum2D.sumRegion(1,1, 2,2)); System.out.println(rangeSum2D.sumRegion(1,2, 2,4)); } }

Complexity Analysis:

Time complexity: O(m *n) where m is the row's length, and n is the column's length of input array matrix when computing prefix sum array. Everytime sumRegion is called, it returns in constant time.
Space complexity: O(m *n ) - space used by the prefix sum array.

Above implementations source code can be found at GitHub link for Java code

Constraints:

Contents

Prefix sum implementation steps:

sumRegion implementation steps:

Complexity Analysis: